Unter
Diskreter Optimierung versteht man die Suche nach einer
optimalen Lösung zu einem Problem mit diskretem Suchraum.
Solche Probleme treten in der Praxis an vielen Stellen auf.
Als Beispiele seien genannt:
- Einplanung von Aufträgen bei Fertigungsstraßen
- Zuteilung von Verbindungen in Kommunikationsnetzwerken
- Berechnung des Chiplayouts bei VLSI
Viele Diskrete Optimierungsprobleme, die in der Praxis auftreten,
lassen sich sehr gut mit Hilfe von Graphen modellieren und
lösen. Aus diesem Grund beschäftigen sich seit mehreren
Jahrzehnten Wissenschaftler aus den Bereichen Informatik und
Mathematik intensiv mit der Entwicklung von Algorithmen zur
effizienten Lösung typischer Problemstellungen für
Graphen. Doch was ist ein effizienter Algorithmus? Gewöhnlich
lassen sich die bei der Diskreten Optimierung betrachteten
Probleme dadurch charakterisieren, dass der Suchraum endlich
ist und somit eine optimale Lösung durch vollständige
Suche gefunden werden könnte. Da der Suchraum jedoch meistens
zwar endlich aber riesig ist (und die exakte Lösung der
Probleme nicht selten NP-schwer ist), muss; man in der Praxis
auf andere Methoden ausweichen. Hierbei gilt es, die Struktur der
zugrundeliegenden Probleme bzw. Graphen bestmöglich
auszunutzen. Oft führt nämlich ein naiver
Lösungsansatz zu einem Algorithmus mit exponentieller
Laufzeit oder zumindest einer Laufzeit, die um einen großen
Faktor langsamer ist als bei Einsatz geschickterer
Methoden. Tatsächlich hat sich gezeigt, dass es für
viele Probleme, bei denen ein naiver Lösungsansatz zu
exponentiellen Laufzeiten führt, doch sehr schnelle
Algorithmen gibt.
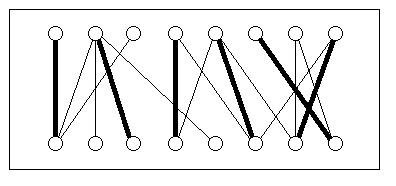
Matching maximaler Kardinalität in einem bipartiten Graphen
Ein Beispiel sind sogenannte Matching-Algorithmen, die viele
unterschiedliche Zuordnungsprobleme lösen können. Ein
solches Problem könnte etwa darin bestehen, Dozenten und
Kurse einander so zuzuordnen, dass möglichst viele Kurse
gehalten werden können. Dabei soll jeder Dozent nur einen
Kurs halten, und jeder Kurs soll nur von einem Dozenten gehalten
werden. In diesem Fall lässt sich das Problem als
bipartiter Graph modellieren (siehe Bild). Die obere Reihe von
Knoten entspricht den Dozenten, die untere Reihe den Kursen. Eine
Kante zwischen einem Dozent und einem Kurs bedeutet, dass der
Dozent fähig ist, den Kurs zu halten. Eine unter diesen
Bedingungen gültige Zuordnung von Dozenten zu Kursen
entspricht genau einem Matching. Im Beispiel können maximal
sechs der acht Kurse gehalten werden, und die fett dargestellten
Kanten entsprechen einer solchen Zuordnung. Der Algorithmus von
Hopcroft und Karp löst das Matching-Problem in bipartiten
Graphen in Zeit
O(sqrt(n)*m), wobei
n die Anzahl der
Knoten und
m die Anzahl der Kanten des Graphen ist.
Im Rahmen des Praktikums sollen Studierenden zu einem
großen Teil verschiedene Graphenalgorithmen effizient
implementieren.
Während Probleme mit kleinen Eingabegrößen in der
Regel auch mit naiven ad hoc Ansätzen gelöst werden
können, zeigen sich die Grenzen derartiger Verfahren bei
steigender Problemgröße und besonders bei
praxisrelevanten Eingabedaten recht schnell. Der Fokus im
Praktikum Diskrete Optimierung liegt daher auf der Lösung von
Problemen mit
großen oder sogar
riesigen
Eingabeinstanzen. Beispiele für im Praktikum zu lösende
Optimierungsprobleme sind:
- Minimale Spannbäme
- Kürzeste Pfade
- Matchings
- Netzwerkfluss
- Färbung planarer Graphen
- Approximation des Traveling Salesman Problem
Neben diesen Graphenproblemen werden aber auch einige Probleme
behandelt, die aus einem anderen Anwendungsbereich kommen und nur
indirekt mit Graphen zu tun haben. Beispiele hierfür sind:
- Suchen von Strings in Texten
- Berechnung der Edit-Distance zweier Strings
Mit dem Praktikum werden mehrere Ziele verfolgt:
- Tieferes Verständnis der Methoden zur Diskreten Optimierung,
- Erfahrungen bei der Entwicklung hochoptimierter Software für
rechenintensive Probleme.
- Spaß an der Herausforderung, die bestmögliche Leistung
aus dem verfügbaren Rechensystem "herauszukitzeln".
Viele der Algorithmen werden in den Vorlesungen
Effiziente
Algorithmen und Datenstrukturen
und
Effiziente Algorithmen
und Datenstrukturen II
besprochen. Die Vorkenntnisse aus
diesem Veranstaltungen sind nützlich, können aber auch
parallel zum Praktikum erworben werden. Auf spezielle Fragen,
welche die Implementierung betreffen und in den Vorlesungen nur
knapp behandelt werden, wird in der Praktikumsbesprechung
eingegangen.
Unter anderem enthalten folgende Bücher Beschreibungen der im
Praktikum zu implementierenden Algorithmen:
- Cormen, Leiserson, Rivest. Introduction to Algorithms. MIT Press, 1990
- Turau. Algorithmische Graphentheorie. Addison Wesley, 1996
- Gibbons. Algorithmic Graph Theory. Cambridge University Press, 1985
- Mehlhorn. Data structures and algorithms 2: Graph algorithms and NP-Completeness. Springer-Verlag, 1984
- Papadimitriou, Steiglitz. Combinatorial Optimization: Algorithms and complexity. Prentice-Hall, 1982
- Sedgewick. Algorithms. Addison-Wesley, 1988
- Tarjan. Data Structures and Network Algorithms. SIAM, 1983
- Reingold, Nievergelt, Deo. Combinatorial Algorithms. Prentice-Hall, 1977
- Ahuja, Magnanti, Orlin. Network Flows: Theory, Algorithms, and Applications. Prentice Hall, 1993





