Load Balancing for Problems with Good Bisectors,
and Applications in Finite Element Simulations
This paper studies load balancing issues for classes of problems
with certain bisection properties.
A class of problems has 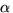 -bisectors
if every problem in the class can be subdivided into two subproblems
whose weight is not smaller than an
-bisectors
if every problem in the class can be subdivided into two subproblems
whose weight is not smaller than an 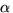 -fraction of the original
problem. It is shown that the maximum weight of a subproblem produced by
Algorithm HF, which partitions a given problem
into N subproblems by always subdividing the problem with
maximum weight, is at most a factor of
-fraction of the original
problem. It is shown that the maximum weight of a subproblem produced by
Algorithm HF, which partitions a given problem
into N subproblems by always subdividing the problem with
maximum weight, is at most a factor of
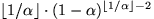 greater than the theoretical optimum (uniform partition).
This bound is proved to be asymptotically tight.
Two strategies to use Algorithm HF
for load balancing distributed hierarchical finite element simulations
and experimental results are
presented. For this purpose, a certain class
of weighted binary trees representing the load of such applications
is shown to have 1/4-bisectors.
This establishes a performance guarantee of 9/4 for load
balancing in this case.
greater than the theoretical optimum (uniform partition).
This bound is proved to be asymptotically tight.
Two strategies to use Algorithm HF
for load balancing distributed hierarchical finite element simulations
and experimental results are
presented. For this purpose, a certain class
of weighted binary trees representing the load of such applications
is shown to have 1/4-bisectors.
This establishes a performance guarantee of 9/4 for load
balancing in this case.
![]() -bisectors
if every problem in the class can be subdivided into two subproblems
whose weight is not smaller than an
-bisectors
if every problem in the class can be subdivided into two subproblems
whose weight is not smaller than an ![]() -fraction of the original
problem. It is shown that the maximum weight of a subproblem produced by
Algorithm HF, which partitions a given problem
into N subproblems by always subdividing the problem with
maximum weight, is at most a factor of
-fraction of the original
problem. It is shown that the maximum weight of a subproblem produced by
Algorithm HF, which partitions a given problem
into N subproblems by always subdividing the problem with
maximum weight, is at most a factor of
![]() greater than the theoretical optimum (uniform partition).
This bound is proved to be asymptotically tight.
Two strategies to use Algorithm HF
for load balancing distributed hierarchical finite element simulations
and experimental results are
presented. For this purpose, a certain class
of weighted binary trees representing the load of such applications
is shown to have 1/4-bisectors.
This establishes a performance guarantee of 9/4 for load
balancing in this case.
greater than the theoretical optimum (uniform partition).
This bound is proved to be asymptotically tight.
Two strategies to use Algorithm HF
for load balancing distributed hierarchical finite element simulations
and experimental results are
presented. For this purpose, a certain class
of weighted binary trees representing the load of such applications
is shown to have 1/4-bisectors.
This establishes a performance guarantee of 9/4 for load
balancing in this case.