Parallel Load Balancing for Problems with Good Bisectors
This paper studies parallel load balancing algorithms for classes of
problems with certain bisection properties. A class of problems has
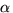-bisectors if every problem p of weight
w(p)
in the class can be subdivided into two subproblems
whose weight (load) is
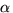at least an -fraction of the original problem. The
task is to split a problem p into N subproblems such that the
maximum weight among them is as close to
w(p)/N as possible.
It was previously known that good load balancing
can be achieved for such classes of problems using Algorithm HF, a
sequential algorithm that repeatedly bisects the subproblem with maximum
weight.
In the present paper, parallel algorithms for this load balancing
problem are introduced: first, a parallel implementation of Algorithm HF
is derived; second, a simpler and faster parallel algorithm requiring
less communication overhead, Algorithm BA, is presented. Both
algorithms are analyzed with respect to worst-case load imbalance,
running-time, and communication overhead. Then an integration of the
two, Algorithm BA-HF, is shown to combine advantages of both
approaches. Finally, the results of extensive simulation experiments
regarding the load imbalance incurred by the three algorithms
in the average case are reported.
