|
|
Forschungsschwerpunkte des Teilprojekts A7 |
Im einzelnen wurden und werden folgende Forschungsthemen aufgegriffen und untersucht:
Auch gilt es zu untersuchen, in welchen Fällen und wie Dynamisches Programmieren parallel implementiert werden kann, ohne eine (zwar polynomielle, aber) übermäßige Anzahl von Prozessoren zu verwenden. Es besteht auch die Hoffnung, Techniken, die für die effiziente Implementierung von Divide-and-Conquer entwickelt werden, auf Probleme der baumartigen Suche (z.B. minmax, alpha-beta) zu übertragen. Schließlich ist beabsichtigt, bekannte (PRAM) Techniken für loop unrolling auf die betrachteten Netzwerktopologien zu übertragen und gegebenenfalls neue Algorithmen dafür zu entwickeln.
Ein paar interessante Teilergebnisse sollten hierzu noch erwähnt werden: es stellte sich zum einen heraus, daß die bei der Baumauswertung erforderliche Kommunikation auf dem Hyperwürfel zu einem logarithmischen Overhead in der zu leistenden Gesamtarbeit führt, die Zeitkomplexität bei p Prozessoren und Eingabelänge n also Omega(n*log(n)/p) ist, während sequentiell natürlich nur lineare Arbeit erforderlich ist.
Das zweite Teilergebnis betrifft das Term Matching Problem, das ein Spezialfall des grundsätzlichen Problems der Unifikation logischer Ausdrücke ist und in der logischen Programmierung und in Termersetzungssystemen immer wieder auftritt. Ein Term ist hier ein Ausdruck, der sich aus Funktionssymbolen (beliebiger Stellenzahl), Konstanten und Variablen zusammensetzt. Die Eingabe für ein Term Matching Problem besteht aus zwei Termen A und B, wobei B keine Variablensymbole enthält. Die Aufgabenstellung besteht darin, für die Variablen im Term A eine Substitution zu finden, so daß durch sie A identisch zu B wird. Als Beispiel betrachte man etwa die Terme
Paterson und Wegman haben einen sequentiellen Algorithmus mit linearem Zeitbedarf für das allgemeine Unifikationsproblem angegeben, das dann später von Dwork, Kanellakis und Mitchell als P-vollständig und damit als höchstwahrscheinlich nicht effizient parallelisierbar nachgewiesen wurde. Die ersten parallelen Algorithmen für das Term Matching Problem mit optimalem Speedup und logarithmischer Laufzeit gehen auf Kedem und Palem zurück. Die dabei verwendeten Maschinenmodelle sind die CRCW-PRAM und die randomisierte CRCW-PRAM. Für das CREW-PRAM Modell haben Kosaraju und Delcher einen arbeitsoptimalen Algorithmus mit logarithmischer Laufzeit für das Term Matching Problem entwickelt, dessen Ansatz dem unsrigen in [MW95a] sehr ähnlich ist.
Das Term Matching Problem zerfällt ganz natürlich in zwei Phasen. In der ersten Phase werden alle Paare einander entsprechender Symbole in den Termen A und B betrachtet, wobei die Entsprechung durch die Position in den geordneten Bäumen gegeben ist, die die beiden Terme A und B darstellen. Da die Symbole in A in der gleichen Reihenfolge erscheinen wie die entsprechenden Symbole in B, genügt ein monotones Routing (die Routine, die auch ein Kernstück unseres optimalen Divide-and-Conquer-Algorithmus darstellt), um entsprechende Symbole zusammenzubringen. Wir nennen diesen Teil des Algorithmus das Term-Angleichungsproblem. In der zweiten Phase des Term Matching Problems werden dann alle Paare entsprechender Symbole und die Unterbäume des zu B gehörigen Baums, die zur selben Variablen gehören, auf Gleichheit überprüft. Hierfür verwenden wir einen Sortieralgorithmus.
Indem wir einen zweistufigen Divide-and-Conquer-Ansatz auf das Term-Angleichungsproblem anwenden, gelingt es uns, dieses Problem für Eingaben der Größe n auf einem Hyperwürfel mit p Prozessoren in Zeit O(n*log(p)/p) zu lösen.
Um bei konkreten Prozessornetzwerken die Kommunikationskosten möglichst gering zu halten, versucht man kommunizierende Prozesse auf möglichst nah beieinanderliegende Prozessoren abzubilden. Dies läßt sich mathematisch mit Hilfe von Grapheinbettungen modellieren. Hierbei repräsentiert der einzubettende Graph (im folgenden Gastgraph genannt) die Kommunikation des Algorithmus, während der Graph, in den eingebettet wird (im folgenden Wirtsgraph genannt), das konkrete Mehrprozessorsystem darstellt. Bei einer Grapheinbettung werden die Knoten bzw. Kanten des Gastgraphen auf Knoten bzw. Pfade des Wirtsgraphen abgebildet. Hierbei sind die Endpunkte eines Pfades, der das Bild einer Kante ist, gerade die Bilder der inzidenten Knoten zu dieser Kante. Die Güte einer Einbettung wird durch die folgenden Maße charakterisiert: die Dilation ist der maximale Abstand zweier im Gastgraphen adjazenter Knoten im Wirtsgraphen; die Expansion ist das Verhältnis der Knotenanzahl des Wirtsgraphen zur Anzahl der Knoten des Gastgraphen; die Last ist die maximale Anzahl von Knoten des Gastgraphen, die auf einen Knoten des Wirtsgraphen abgebildet werden; die Kanten-Belastung ist die maximale Anzahl von Pfaden, die Bilder von Kanten des Gastgraphen sind und über eine Kante des Wirtsgraphen gehen; die Knoten-Belastung ist die maximale Anzahl von Pfaden, die Bilder von Kanten des Gastgraphen sind und einen Knoten des Wirtsgraphen beinhalten.
Um eine gute Auslastung des Mehrprozessorsystems zu haben, ist man an einer möglichst kleinen Expansion interessiert, da ansonsten zu viele Prozessoren des Parallelrechners überhaupt nicht in Betracht gezogen werden. Ebenso sollte die Last so klein wie möglich sein (am besten etwa max{1,M/N}, wobei M die Anzahl der Prozesse, d.h. die Anzahl der Knoten im Gastgraphen, und N die Anzahl der Prozessoren, d.h. die Anzahl der Knoten im Wirtsgraphen, ist). Unter diesen Nebenbedingungen sucht man nun nach Einbettungen mit möglichst kleiner Dilation. Die Dilation beschränkt zum einen die Dauer einer Kommunikation zwischen zwei kommunizierenden Prozessen, und zum anderen die Gesamtzahl der zur Kommunikation benutzten Verbindungen im Mehrprozessorsystem. Um eine möglichst geringe Anzahl von Konflikten beim Zustellen der Nachrichten zu bekommen, sollte die Knoten- und Kanten-Belastung ebenfalls möglichst gering sein.
Hat man eine gute Einbettung gefunden, so kennt man die Wege, auf denen die Nachrichten zu transportieren sind. Um aber Staus an Kanten bzw. Knoten vermeiden zu können, benötigt man auch noch ein Schedule, in dem festgelegt wird, zu welchen Zeitpunkten die Nachrichten über die einzelnen Kanten eines Pfades verschickt werden. Interessanterweise ist diesem Problem in der Literatur zunächst wenig Beachtung geschenkt worden. Leighton, Maggs und Rao (1988, 1994) haben gezeigt, daß sich die Nachrichten in Zeit O(d+l) zustellen lassen, wenn man eine Einbettung mit Dilation d und Kanten-Belastung l hat. Leider war dies ein off-line Algorithmus, der den Schedule mit Hilfe des Lovasz Local Lemmas (also mit Hilfe der probabilistischen Methode) konstruierte. Erst durch die Konstruktion einer algorithmisierten Version des Lovasz Local Lemmas von Beck (1991) und einer Weiterentwicklung zu einer parallelen algorithmischen Version von Alon (1991) konnten Leighton und Maggs (1995) einen paralleler Algorithmus zum Auffinden des Schedules für eine gegebene Einbettung entwickeln. Allerdings ist die Lösung immer noch so komplex, daß sie hauptsächlich von theoretischen Interesse ist. Daher muß zur Simulation von parallelen Algorithmen auf Prozessornetzwerken neben einer Einbettung ebenfalls noch das Scheduling zum Versenden der Nachrichten gefunden werden.
Im folgenden beschränken wir uns zunächst wegen seiner regelmäßigen Struktur auf den Hyperwürfel als Wirtsgraphen. Dieser stellt auch in der Literatur den am meisten untersuchten Wirtsgraphen dar. Für Gastgraphen mit einer regulären Struktur wie z.B. mehrdimensionale Gitter, Binomialbäume, vollständige binäre Bäume, X-Trees, mehrdimensionale Pyramiden, Hyperpyramiden, usw., sind sehr gute Einbettungen gefunden worden, die darüber hinaus (auf Grund der sehr kleinen Dilation) gleichzeitig den Schedule für die Kommunikation mitliefern. Für Einbettungen von Gastgraphen mit einer mehr ungeordneten Struktur, wie z.B. beliebige Bäume, war in der Literatur wenig bekannt. Im wesentlichen gab es Einbettungen für binäre Bäume von Bhatt, Chung, Leighton und Rosenberg (1988, 1992) und von Monien und Sudborough (1988), sowie für deren Sonderfälle, die binären Caterpillars von Havel und Liebl (1986) und von Bezrukov, Monien, Unger und Wechsung (1995).
Im Teilprojekt A7 gelang nun die Entwicklung eines allgemeinen, zweiphasigen Schemas zur Einbettung von Gastgraphen mit einer ungeordneten Struktur in Topologien, die dem Hyperwürfel ähnlich sind ([HM96d], [H96]). Mit Hilfe dieses Schemas lassen sich Einbettungen mit optimaler Expansion und Last 1 erzielen. Die erzielte Dilation und Kanten-Belastung hängen dabei von der Qualität eines erweiterten Kanten-Bisektors des gegebenen Gastgraphen ab. Ein erweiterter Kanten-Bisektor ist ein gewöhnlicher Kanten-Bisektor mit der zusätzlichen Eigenschaft, daß eine gegebene Teilmenge der Knoten möglichst gleichmäßig auf beide Teilgraphen verteilt wird. Die Qualität eines erweiterten Kanten-Bisektors bestimmt sich aus dessen Größe und dem Verhältnis, wie die Knoten der gegebenen Teilmenge auf die beiden Hälften verteilt werden. Zur Einbettung wird als Hilfsstruktur ein (k,h,o,lambda,tau)-Baum (gesprochen cold-Baum, da in diesem die Irregularität der Struktur quasi eingefroren wird) verwendet. Ein (k,h,o,lambda,tau)-Baum ist ein vollständiger 2k-ärer Baum der Höhe h, wobei die Knoten gewichtet sind. Die Knotengewichte selbst werden als Kapazitäten bezeichnet. In der ersten Phase wird nun der Gastgraph in den (k,h,o,lambda,tau)-Baum eingebettet, wobei die Last jedes Knotens des (k,h,o,lambda,tau)-Baumes durch dessen Kapazität beschränkt ist. In dieser Phase der Einbettung wird darauf geachtet, daß adjazente Knoten des Gastgraphen auf Knoten des (k,h,o,lambda,tau)-Baumes abgebildet werden, die möglichst nah beieinander liegen, d.h. daß deren nächster gemeinsamer Vorfahr im (k,h,o,lambda,tau)-Baum möglichst geringen Abstand zu den beiden Knoten hat. Dazu müssen Kanten-Bisektoren möglichst hoher Qualität für die betrachtete Klasse von Graphen zur Verfügung stehen. In der zweiten Phase wird diese Einbettung zu einer Einbettung mit Last 1 in den Hyperwürfel erweitert. Dazu wird eine geschickte Partitionierung der Hyperwürfelknoten ausgenutzt, die jedem Knoten des (k,h,o,lambda,tau)-Baumes eine Menge von Knoten des Hyperwürfels zuweist, so daß die Kardinalität dieser Menge gerade der Kapazität des Knotens im (k,h,o,lambda,tau)-Baum entspricht.
Mit Hilfe dieses Schemas konnten nun für viele, verschiedenste Graphklassen Einbettungen hoher Qualität in den Hyperwürfel konstruiert werden. Es soll hier nochmals betont werden, daß aufgrund des Schemas alle folgenden Einbettungen optimale Expansion (d.h. für den Hyperwürfel Expansion <2, da Hyperwürfel nur in Größen von Zweierpotenzen verfügbar sind) und optimale Last 1 besitzen. Im einzelnen konnte für die Klasse beliebiger binärer Bäume eine Einbettung mit Dilation <=8 bewiesen werden ([HM96a], [H96]). Für die in der Praxis sehr wichtige Klasse der Graphen mit beschränkter Baumweite (auch als Klasse der partiellen k-Bäume bekannt) konnte gezeigt werden, daß sich diese mit Dilation 3*ceil(log((d+1)*(t+1)))+8 einbetten lassen, wobei t die Baumweite und d der maximal Grad des Gastgraphen ist ([HM96], [H96]). Für Graphen mit beschränkter Pfadweite oder beschränkter Kreisweite (Graphen mit beschränkter Kreisweite sind ähnlich definiert wie Graphen mit beschränkter Pfadweite, jedoch wird hier verlangt, daß der Zerlegungsgraph ein Kreis statt eines Pfades sein muß) konnte diese Ergebnis noch verbessert werden. Für Graphen mit Pfadweite oder Kreisweite w und maximalem Grad d gibt es Einbettungen mit Dilation 3*ceil(log((d+1)*(t+1))). Weiterhin konnten für Circular-Arc-Graphen, Intervall-Graphen, k-outerplanare Graphen, planare Graphen, chordale Graphen und Reihen-Parallel-Graphen Einbettungen hoher Güte gefunden werden ([HM96d], [H96]). Aufgrund der konstruierten Einbettungen lassen sich auch Schedules für die verschiedensten Graphklassen sehr schnell herleiten, so daß man nicht mehr auf die komplizierten (und mehr von theoretischen Interesse) Algorithmen von Leighton und Maggs (1995) angewiesen ist.
Auf der anderen Seite konnte auch gezeigt werden, daß sich diese Einbettungen nicht nur konstruieren lassen, sondern daß es sehr effiziente parallele Algorithmen zu deren Berechnung auf dem Hyperwürfel gibt. Die obigen Einbettungen lassen sich in Zeit O(max{(log(N))²,TLR}(N)) berechnen, wenn die anderen Parameter in den oben beschriebenen Einbettungen, wie z.B. der maximale Grad des Gastgraphen, als konstant angenommen werden. Hierbei bezeichne TLR(N) die Zeitkomplexität für die Berechnung von List-Ranking auf einer Liste der Länger Theta(N) auf einen Hyperwürfel mit N Knoten. Der schnellste bekannte Algorithmus für List-Ranking auf dem Hyperwürfel benötigt O( (log(N))² * log(log(log(N))) * logstar(N)) Schritte ([HM93], [HM96a], [H96]).
Das im Teilprojekt A7 entwickelte, zweiphasige Schema ist so vielseitig, daß es sich ebenfalls für eine Vielzahl (wenn nicht sogar aller) vom Hyperwürfel abgeleiteter Topologien verwenden läßt. Es konnte gezeigt werden, daß sich die vorher erwähnten Einbettungen der verschiedensten Graphklassen für die folgenden Topologien modifizieren lassen ([HM96d], [H96]): folded hypercubes (eingeführt von Latifi, El und Amawy (1989)), twisted hypercubes (eingeführt von Hillis (1981) und von Esfahanian, Ni und Sagan (1991)), twisted cubes (eingeführt von Hilbers, Koopman, und van de Snepscheut (1987)), generalized twisted hypercubes (eingeführt von Chedid und Chedid (1993)), multiply-twisted bzw. crossed cubes (eingeführt von Efe (1991, 1992)) und Möbius cubes (eingeführt von Cull und Larson (1995)). Hierbei müssen nur Änderungen der Partitionierung der Knoten der gewählten Wirtstopologie vorgenommen werden, die sich ziemlich direkt aus der entsprechenden Topologie des Wirtsgraphen entnehmen lassen. Für eine andere große Zahl von hyperwürfelähnlichen Wirtstopologien lassen sich die oben erwähnten Einbettungen übertragen, wenn man zusätzlich kleine Modifikationen an der Definition des (k,h,o,lambda,tau)-Baumes vornimmt, die sich aber ebenfalls ziemlich direkt aus den Definitionen der entsprechenden Topologien ablesen lassen ([HM96d], [H96]): generalized hypercubes, incomplete hypercubes (eingeführt von Katseff(1988)), Fibonacci cubes (eingeführt von Hsu (1993)), die Familie der Mcubes (eingeführt von Singhvi (1993)), folded Petersen networks und folded Petersen cubes (eingeführt von Oehring und Das (1993)), und star graphs (eingeführt von Akers, Harel und Krishnamurthy (1987)).
Von Bhatt und Cai (1988, 1993) wurde bereits ein randomisiertes Verfahren zur Einbettung binärer Bäume in den Hyperwürfel mit Dilation O(log(log(N))) vorgestellt, wobei N die Anzahle der Knoten im Hyperwürfel ist. Von Leighton, Newman, Ranade und Schwabe (1989, 1992) wurde dann eine dynamische Einbettung binärer Hyperwürfel mit konstanter Dilation vorgestellt. Mit großer Wahrscheinlichkeit wird konstante Last und konstante Kanten-Belastung erreicht. Die erreichte Dilation kann nach Leighton (1992) bis auf 8 gedrückt werden.
Im Teilprojekt A7 wurde nun ein deterministischer Algorithmus zur dynamischen Einbettung binärer Bäume gefunden, der Migration verwendet. Der entwickelte Algorithmus basiert auf dem zweiphasigen Schema der statischen Einbettungen. Als Hilfsstruktur wird hierfür ein modifizierter, den Gegebenheiten angepaßter (k,h,o,lambda,tau)-Baum verwendet, der sogenannte (h,o,tau)-Baum (gesprochen hot-Baum, da in diesem (h,o,tau)-Baum die Knoten wegen ihrer Beweglichkeit immer auf hoher Temperatur gehalten werden müssen). Die gefundene dynamische Einbettung erzielt zu jedem Zeitpunkt bessere Güten als der beste bislang bekannte Algorithmus von Leighton, Newman, Ranade und Schwabe (1989, 1992). Darüber hinaus ist die amortisierte Laufzeit zur Einbettung eines einzelnen Knotens konstant. Dies ist ein wesentlicher Vorteil gegenüber dem Algorithmus von Leighton, Newman, Ranade und Schwabe (1989, 1992), da es in diesem Algorithmus nicht klar ist, wie ein neuer Knoten in konstanter oder auch nur in konstanter amortisierter Zeit eingefügt werden kann. Betrachtet man den Fall, daß in jedem Schritt maximal B neue Blätter in den binären Baum eingefügt werden, so beträgt die amortisierte Laufzeit O((log(B))²) für jede solche Gruppe von maximal B Blättern. Auch dies ist eine Verbesserung gegenüber dem Algorithmus von Leighton, Newman, Ranade und Schwabe (1989, 1992), da hier das Einfügen von mehreren Blättern zu Schreibkonflikten führen kann. Es ist nicht klar, wie der Algorithmus von Leighton, Newman, Ranade und Schwabe (1989, 1992) erweitert werden kann, um solche Schreibkonflikte effizient zu vermeiden.
Es bestehen wohlbegründete Hoffnungen, daß sich der im Teilprojekt A7 entwickelte deterministische Algorithmus zumindest für Einbettungen von Graphen mit beschränkter Baumweite erweitern läßt. Darüber hinaus sollte er sich auch für Einbettungen in die dem Hyperwürfel ähnlichen Topologien anpassen lassen.
Für den speziellen Fall der dynamischen Einbettung eines vollständigen binären Baumes konnte ebenfalls ein effizienter dynamischer Algorithmus im Teilprojekt A7 entwickelt werden ([HM96b], [H96]). Jeder neue vollständige Level des wachsenden vollständigen binären Baumes kann dabei in konstanter Zeit auf dem Hyperwürfel selbst eingebettet werden. Dieser Algorithmus kommt in diesem Spezialfall ohne Randomisierung und Migration aus, wenn man mit einer Expansion <4 während der gesamten Einbettung zufrieden ist. Für eine Einbettung in den optimalen Hyperwürfel (also mit Expansion <2) muß in jedem Schritt die Hälfte der alten Blätter neu eingebettet werden, was auch optimal ist.
Dabei gelang es, effiziente parallele Algorithmen für das Scheduling von Tasksystemen mit Tasks einheitlicher Ausführungsdauer und mit Präzedenzrelationen zu finden, die Intervallordnungen darstellen. Intervallordnungen sind partielle Ordnungen, die durch Intervall-Darstellungen gegeben werden können. Dabei entspricht jeder Task in dem Schedulingproblem einem geschlossenen Intervall auf der reellen Achse, und ein Task muß nach einem anderen Task geschedult werden, wenn sein Intervall gänzlich rechts von dem Intervall des anderen Tasks liegt (Bemerkung: die den Tasks zugeordneten Intervalle haben nichts etwa mit Zeitintervallen zu tun, während deren die Tasks ausführbar sind, sondern dienen dazu, die gegenseitige Abhängigkeit der Tasks darzustellen). Die Klasse der Intervallordnungen ist recht reich und hat in der Literatur umfangreiche Betrachtung gefunden, siehe etwa die Arbeiten von Fishburn (1985) und von Naor, Naor und Schäffer (1989). Sie kommen z.B. in natürlicher Weise als Präzedenzrelation in Assemblierungsproblemen vor. Folgendes Bild zeigt ein Beispiel.
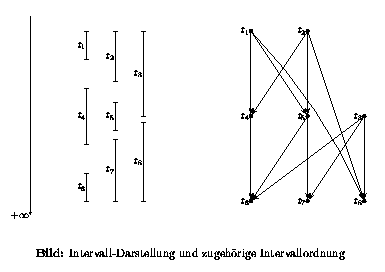
Für das Schedulingproblem auf Intervallordnungen mit Tasks einheitlicher Ausführungsdauer ist ein optimaler sequentieller Algorithmus bekannt (Papadimitriou und Yannakakis, 1979), der lineare Laufzeit benötigt. Läßt man die Bedingung der einheitlichen Ausführungsdauer weg, wird das Schedulingproblem NP-vollständig. Der erwähnte sequentielle Algorithmus basiert auf dem Ansatz des List Schedulings und erscheint inhärent sequentiell. In der Tat ist das allgemeine List Scheduling Problem P-vollständig (Helmbold und Mayr, 1987; Sunder und He, 1993) und damit höchstwahrscheinlich nicht effizient parallelisierbar.
In [M96] haben wir einen NC-Algorithmus für das Problem angegeben, für ein System von Tasks einheitlicher Ausführungsdauer und mit einer Intervallordnung als Präzedenzrelation einen optimalen Schedule minimaler Länge auf einer beliebigen, in der Eingabe vorgegebenen Anzahl paralleler Prozessoren zu finden. Dieser Algorithmus läuft selbst auf einer CREW-PRAM mit n³ Prozessoren in Zeit O((log(n))²) und stellt damit einen wesentlichen Fortschritt gegenüber dem einzigen vorher bekannten Algorithmus von Sunder und He (1993) dar.
Unser Algorithmus ist in zweierlei Hinsicht bemerkenswert. Zum einen stellt er eines der wenigen Beispiele eines Schedulingproblems dar, wo für eine nicht-konstante Anzahl von Prozessoren überhaupt ein NC-Algorithmus gefunden worden ist. Zum anderen stellt sich heraus, daß unser Algorithmus die gleiche Lösung berechnet (allerdings parallel und auf gänzlich anderem Wege) wie der auf List Scheduling basierende sequentielle Algorithmus von Papadimitriou und Yannakakis (1979).
Kann dieses Grundproblem gelöst werden, so steht uns eine sehr praktische Methode für die Entwicklung paralleler Programme zur Verfügung. Der Algorithmus wird dabei auf einer sehr hohen Ebene formuliert, unabhängig von einer spezifischen Hardwarearchitektur. Dann wird dieses Programm in einen Zwischencode übersetzt, der sich auf die kausalen Zusammenhänge zwischen den atomaren Berechnungen konzentriert. Im letzten Schritt wird aus dem Zwischencode ein Schedule berechnet, der für eine konkrete parallele Maschine mit gegebener Anzahl von Prozessoren und einem spezifischen Kommunikationsnetzwerk abgestimmt ist.
Ein prominentes Beispiel für dieses Verfahren ist NESL, eine funktionale, daten-parallele Programmiersprache (Blelloch, 1994). NESL erlaubt Parallelität durch die parallele Anwendung von Funktionen auf alle Elemente einer Sequenz, auch dann, wenn die Funktion selbst parallel ist und die Datenelemente der Sequenz wieder aus Sequenzen bestehen. Der vom NESL-Compiler erzeugte Zwischencode läßt sich auf einer ganzen Reihe von parallelen Rechnern ausführen. Obwohl bereits eine Reihe von Ergebnissen in dem Bereich des Schedulings von parallelen Programmen erzielt wurden -- nicht zuletzt auch durch die Forschergruppe um NESL (Blelloch, 1995) -- sind doch noch eine große Zahl von Fragen offen.
Da die Menge der atomaren Berechnungen und die Datenabhängigkeiten zwischen ihnen oft erst zur Laufzeit eines parallelen Programms bekannt werden, ist es unabdingbar, den Schedule selbst ebenfalls parallel zu berechnen. Dabei lassen sich verschiedene Klassen von Scheduling-Problemen identifizieren. Werden die atomaren Berechnungen und die Datenabhängigkeiten zwischen ihnen erst während des Ablaufs eines parallelen Programms bekannt, handelt es sich um online-Schedulingprobleme. Ist dagegen die Ablaufstruktur des Programms a priori bekannt, so sprechen wir von offline-Problemen. Ein weiteres Merkmal ergibt sich aus dem Kommunikationsnetzwerk des Rechners für den der Schedule berechnet werden soll. Handelt es sich um einen Rechner mit Shared-Memory, so muß der Schedule keine Rücksicht auf den Transport der Daten zwischen den atomaren Berechnungen nehmen. Handelt es sich dagegen um einen Rechner mit nicht vernachlässigbaren Kommunikationszeiten zwischen den einzelnen Prozessoren, so muß der Schedule die Verzögerung der Daten, die bei der Kommunikation entsteht, mit in den Schedule einplanen.
Im Teilprojekt A7 wurde eine Reihe von grundlegenden Problemen in diesem Bereich angegangen. Untersucht wurden zuerst Problemklassen, die sequentiell einfach zu berechnen sind. Erste Erfolge wurden beim Scheduling mit baumartigen Präzedenzen und einheitlich langen Tasks erzielt. Dieses Problem hat eine lange Geschichte, die mit dem aufkommenden Interesse an der Auswertung von mathematischen Formeln und der Automatisierung von Produktionsprozessen in den sechziger Jahren begann. Bereits 1961 stellte Hu einen polynomiellen Algorithmus vor, der optimale Schedules erzeugt. Brucker, Garey und Johnson (1977) zeigten später, daß das Problem sogar in linearer Zeit gelöst werden kann. Später beschäftigten sich eine Reihe von Forschern auch mit parallelen Algorithmen für dieses Problem (Helmbold und Mayr, 1987; Dolev, Upfal und Warmuth, 1986). Dabei zeigte sich, daß es erheblich mehr Mühe bereitet, einen effizienten parallelen Algorithmus zu finden, als die lineare sequentielle Lösung vermuten läßt. Die besten bisher bekannten parallelen Algorithmen benötigen entweder O(log(n)) Zeit und n² Prozessoren oder O((log(n))²) Zeit und n Prozessoren. In [MS96] stellten wir zwei neue parallele Algorithmen vor. Der eine berechnet einen optimalen m-Prozessor Schedule in Zeit O(log(n)) auf n/log(n) Prozessoren, sofern m konstant ist. Für diesen eingeschränkten Fall können wir somit den asymptotischen Arbeitsaufwand des sequentiellen Algorithmus erreichen. Der zweite Algorithmus löst das gleiche Problem in Zeit O(log(n)*log(m)) auf n/log(m) Prozessoren und wendet daher nur O(n*log(n)) Arbeit auf. Obwohl noch nicht arbeitsoptimal, so stellt der Algorithmus doch einen wesentlichen Schritt in diese Richtung dar.
Eine weitere Schwierigkeit ist die Tatsache, daß oftmals keine vollständige Information über die Jobs zur Verfügung steht. Einerseits kann die Laufzeit eines Jobs unbekannt sein. Zum anderen können auch die Präzedenzen zwischen den einzelnen Jobs unbekannt sein. Dies bedeutet, daß der Scheduling-Algorithmus seine Entscheidungen on-line treffen muß. Ein gutes Beispiel hierfür liefert die parallele Berechnung eines Divide-and-Conquer-Algorithmus. In vielen Fällen ist weder die Laufzeit des Divide- oder des Conquer-Schrittes für ein zu lösendes Teilproblem noch die Anzahl der im Divide-Schritt entstehenden neuen Teilprobleme bekannt. Zudem brauchen kleine Teilprobleme in der Regel auch weniger Prozessoren zu ihrer Bearbeitung.
Die Güte eines on-line Algorithmus wird durch die competitive-ratio gemessen (Sleator und Tarjan, 1985). Bei on-line Scheduling-Algorithmen, deren Optimierungsziel ein möglichst kurzer Schedule ist, vergleicht man dazu die Schedule-Länge eines on-line Algorithmus mit der Länge eines optimalen Schedule und maximiert dieses Verhältnis über alle möglichen Eingaben (worst-case Analyse). Ein on-line Algorithmus heißt optimal, wenn es keinen anderen on-line Algorithmus mit besserer competitive-ratio gibt. Der Nachweis der Optimalität wird meist durch untere Schranken (resp. obere Schranken bei Maximierungsproblemen) für den Wert der Zielfunktion geführt, die für jeden deterministischen (oder randomisierten) on-line Algorithmus gelten.
Ein wichtiges Unterscheidungsmerkmal für Scheduling-Strategien ist die Unterbrechbarkeit eines laufenden Jobs. Die Unterbrechung eines parallelen Jobs ist jedoch mit einem sehr hohen Aufwand verbunden (Nachrichten konsistent halten, Datensicherung) und der entstehende Overhead kann keinesfalls vernachlässigt werden. Aus diesem Grund beschränken wir uns auf nicht-unterbrechende (non-preemptive) Scheduling-Algorithmen.
Eine Reihe von Ergebnissen für das on-line Scheduling paralleler Jobs mit Präzedenzen enthalten (Feldmann, Kao, Sgall und Teng, 1993; Sgall, 1994). Für beliebige Rechnertopologien konnte gezeigt werden, daß jeder deterministische on-line Algorithmus für dieses Scheduling-Problem competitive-ratio mindestens N besitzt, wenn N die Anzahl der Prozessoren bezeichnet. Auch Randomisierung kann dieses negative Resultat nicht nennenswert verbessern. Ein Ausweg zur Verbesserung der Performance ist die Beschränkung der maximalen Jobgröße auf lambda*N, 0 < lambda < 1, Prozessoren. Dies liefert eine untere Schranke von 1+(1/(1-lambda)) für die competitive-ratio jedes deterministischen on-line Scheduling-Algorithmus, die auch mit einem Greedy-Algorithmus erreicht wird. Für lambda=½ erhält man somit beispielsweise einen 3-competitiven Algorithmus. Nachteilig ist freilich die Größenbeschränkung für Jobs, die alle Prozessoren auslasten könnten. Eine weitere Möglichkeit zur Performancesteigerung ist die Verwendung von Virtualisierung. Diese Technik erlaubt es, einen Job J nicht auf der verlangten Prozessorzahl k sondern auf einer kleineren Anzahl k' von Prozessoren auszuführen. J wird also auf einer virtuellen Maschine mit k Prozessoren ausgeführt, die von k' Prozessoren simuliert wird. Dadurch verlängert sich natürlich die Laufzeit von J entsprechend der geringeren Prozessorzahl und des Simulations-Overheads. Geht man von der optimistischen Erwartung aus, daß der Slowdown durch die Virtualisierung k/k' beträgt, so kann gezeigt werden, daß es einen optimalen on-line Algorithmus mit competitive-ratio 2+Phi gibt, wobei Phi=(sqrt(5)-1)/2 der goldene Schnitt ist. Kombiniert man Virtualisierung und Beschränkung der maximalen Prozessorzahl, so kann die competitive-ratio auf 2+(sqrt(4*lambda²+1)-1)/(2*lambda) verbessert werden.
Im Rahmen des Teilprojektes A7 wurden weitere Varianten des on-line Scheduling paralleler Jobs mit Präzedenzen untersucht, die Algorithmen mit akzeptabler competitive-ratio zulassen. Dabei wurde zunächst das complete-Modell zugrunde gelegt und die Einschränkung betrachtet, daß alle Jobs unabhängig von ihrer Größe (also der verlangten Prozessorzahl) die gleiche Ausführungszeit haben (UET-Modell). Bekanntlich ist dieses Problem im off-line Fall schon für sequentielle Jobs und Kombinationen von in-forests und out-forests NP-schwer (Garey, Johnson, Tarjan und Yannakakis, 1983), wenn die Anzahl der Prozessoren variabel ist. Ein weiteres interessantes Modell ist das Scheduling mit restricted runtime-ratio. Man beschränkt hierbei das Verhältnis der Ausführungszeit des längsten zum kürzesten Job durch einen Parameter T, der jedoch dem on-line Scheduler nicht bekannt ist. In allen Varianten werden beliebige Präzedenzen zugelassen, da die Beweise der unteren Schranken nur out-forests verwenden.
Für die beiden genannten Varianten konnten im Teilprojekt A7 nahezu (bis auf kleine additive Konstanten) optimale on-line Scheduling-Algorithmen entwickelt werden (Bischof und Mayr, in Vorbereitung), die im folgenden kurz beschrieben werden sollen.
Gegeben sei ein Multiprozessorsystem mit N identischen Prozessoren, das den Annahmen des complete-Modells genügt, eine Menge J von parallelen Jobs mit Laufzeit 1 und eine Partialordnung "<" auf J, die die Präzedenzen zwischen den Jobs kennzeichnet. Ist J1 < J2 für J1, J2 in J, so muß J1 vollständig ausgeführt worden sein, bevor J2 gestartet werden kann. Das Paar (J,<) heißt Job-System. Es ist die Aufgabe des Scheduling-Algorithmus, jedem Job einen Zeitschritt und die verlangte Prozessorzahl zuzuweisen, so daß keine Präzedenzen verletzt werden und in keinem Zeitschritt mehr Prozessoren als vorhanden verwendet werden. Ein Job J heißt verfügbar, wenn alle seine Vorgänger zugewiesen wurden und terminiert haben. Ein on-line Scheduling-Algorithmus hat nur Kenntnis von verfügbaren Jobs.
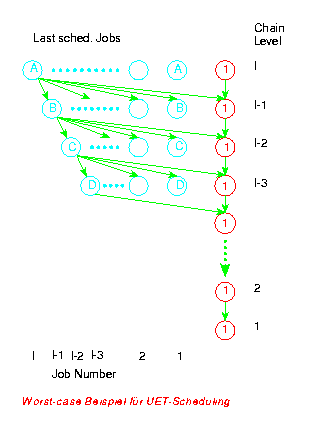
Der Level-Algorithmus weist in jeder Phase alle zu Beginn dieser Phase verfügbaren Jobs Zeitschritten zu und sammelt alle Nachfolgerdieser Jobs, die im Lauf der Phase verfügbar werden. Werden während einer Phase keine Jobs verfügbar, so terminiert der Level-Algorithmus.
Da die Jobs einer Phase (Level) untereinander nicht in Präzedenz stehen, können sie in beliebiger Reihenfolge zugewiesen werden. Damit entsteht pro Phase ein Bin-Packing Problem, wobei die Jobs den zu packenden Elementen und die Zeitschritte den Bins entsprechen. Da auch dieses Problem NP-schwer ist (Garey und Johnson, 1979), wird man zur Berechnung einer Lösung einen der bekannten Approximations-Algorithmen verwenden (Next-Fit, First-Fit, First-Fit-Decreasing).
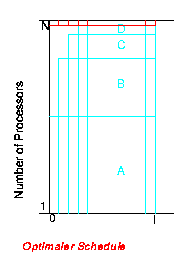
Es konnte gezeigt werden, daß Level(Next-Fit) 3-competitive ist und Level(First-Fit) sogar competitive-ratio 2.7 besitzt. Die Analyse des Level-Algorithmus mit der First-Fit Bin-Packing Strategie ist dabei erheblich aufwendiger und basiert auf den Ergebnissen von Garey, Graham, Johnson und Yao (1976). Da die untere Schranke für die asymptotische (N gegen unendlich) competitive-ratio jedes deterministischen on-line Schedulers 2.691 beträgt, ist Level(First-Fit) ein nahezu optimaler on-line Algorithmus.
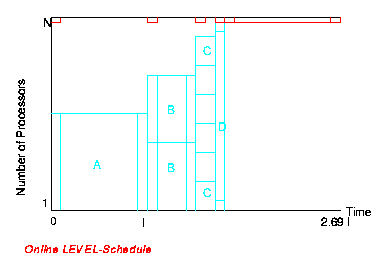
Die schlechte competitive-ratio für das on-line Scheduling paralleler Jobs mit Präzedenzen beruht wesentlich auf der Tatsache, daß große Jobs, die lange nicht zugewiesen werden konnten (da nicht genügend Prozessoren frei waren), nur sehr kurze Laufzeit aufweisen können und die Ausführung weiterer Jobs, zu denen sie in Präzedenz stehen, verzögern. Durch Virtualisierung und Beschränkung der maximalen Prozessorzahl kann diese Konstellation weitgehend vermieden werden. Beide Techniken bringen aber, wie bereits erläutert, auch Nachteile mit sich. Daher untersuchte das Teilprojekt A7 das on-line Scheduling mit restricted runtime-ratio RRR.
In vielen praktischen Anwendungen sind obere und untere Schranken für die Laufzeit eines Jobs a priori bekannt. Somit ist es möglich, das Verhältnis der Laufzeit des längsten zum kürzesten Job eines Job-Systems von oben her durch einen Parameter T=T(J) zu beschränken. Da dieser Wert jedoch kaum exakt bestimmt werden kann, ist es wenig sinnvoll, T dem on-line Scheduler als Eingabe zur Verfügung zu stellen. Ein sehr einfaches Job-System zeigt, daß kein deterministischer on-line Algorithmus für dieses Problem eine competitive-ratio besser als (T+1)/2 haben kann. Der RRR-Algorithmus hat competitive-ratio T/2 + 5.5 und erreicht damit die untere Schranke bis auf eine additive Konstante. Dieses Resultat zeigt, daß T=o(N) eine notwendige Bedingung für den erfolgreichen Einsatz des RRR-Algorithmus ist. Es ist zu betonen, daß der RRR-Algorithmus in seiner adaptiven Version keine Informationen über das Job-System benötigt. Dardurch wird klar, daß die Kenntnis von T für den on-line Scheduler nicht erforderlich ist.
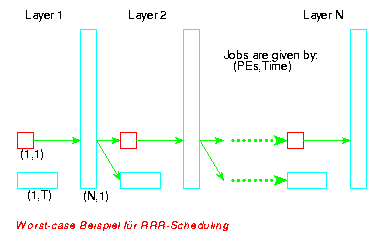
Wesentlich für den RRR-Algorithmus ist die Unterscheidung zwischen großen Jobs, die mehr als die Hälfte der verfügbaren Prozessoren verlangen, und den verbleibenden, kleinen Jobs. Große Jobs werden vom RRR-Algorithmus bevorzugt und exklusiv zugewiesen. Sind zu einem Zeitpunkt t nicht genügend Prozessoren zur Ausführung (irgendeines) großen Jobs frei, so wird entsprechend der Auslastung alpha(t) des Systems, also der Zahl der belegten Prozessoren dividiert durch N, verfahren. Ist alpha(t) < ½, so werden keine kleinen Jobs zugewiesen bis genügend Prozessoren frei sind, um einen großen Job zuweisen zu können. Im Fall alpha(t)>=½ werden verfügbare kleine Jobs greedy zugewiesen. Ebenso wird verfahren, wenn keine großen Jobs verfügbar sind. Abschließend sei bemerkt, daß der RRR-Algorithmus durch seine Struktur in der Lage ist, eine nicht-triviale obere Schranke für die tatsächlich erreichte Performance mitzuberechnen.
In allen diesen Bereichen wird gegenwärtig auf internationaler Ebene intensiv Forschung betrieben, die hier kurz beschrieben werden soll. Untersuchungen zur Zugangskontrolle wurden von Awerbuch, Gawlick, Leighton und Rabani (1994), von Awerbuch, Bartal, Fiat und Rosen (1994) und von Kamath, Palmon und Plotkin (1996) durchgeführt: es wurden Online-Algorithmen mit logarithmischer bzw. polylogarithmischer Güte in bezug auf die Zahl der zustande kommenden Verbindungen für Netzwerke mit Baum-, Gitter- und Hyperwürfeltopologie vorgestellt. Während diese Arbeiten davon ausgehen, daß jede Verbindung sofort abgelehnt oder eingerichtet werden muß, nimmt man beim Scheduling von Verbindungen an, daß alle Verbindungen zustande kommen müssen, aber falls nötig verzögert werden können (Feldmann, 1994, 1995). Zu den bekannten Ergebnissen zählen vor allem Online-Algorithmen mit logarithmischer Güte für Binärbäume, mit polylogarithmischer Güte für Gitter und mit konstanter Güte für Ketten. Fragen des Routing führen bei ATM-Netzen und optischen Netzen unter anderem zum Problem der kantendisjunkten Pfade. Neue Online- und Offline-Algorithmen für kantendisjunkte Pfade in gitterähnlichen Graphen werden von Kleinberg und Tardos (1995) präsentiert. Dabei wird online logarithmische Güte und offline konstante Güte erzielt. Das Online-Ergebnis verbessert damit den Zugangskontrollalgorithmus von Awerbuch, Gawlick, Leighton und Rabani (1994). Weiterhin werden auch Algorithmen untersucht, die das Routing so wählen, daß die durch Verbindungen erzeugte Last möglichst gleichmäßig auf die Links des Netzwerks verteilt wird (Awerbuch, Azar, Plotkin und Waarts, 1994). Für die Wellenlängenzuteilung in optischen Netzwerken mit Baumstruktur wurde in Arbeiten von Raghavan und Upfal (1994), von Mihail, Kaklamanis und Rao (1995), von Kaklamanis und Persiano (1996) und von Kumar und Schwabe (1997) polynomielle Approximationsalgorithmen entwickelt. Der bisher beste Algorithmus kommt mit 7L/4 Wellenlängen aus, wobei L die maximale Zahl von Verbindungen ist, die denselben gerichteten Link benutzen, und damit eine untere Schranke für die optimale Wellenlängenzuteilung darstellt.
Im Rahmen des Teilprojekts A7 wurde das Schedulingproblem für Verbindungen in verschiedenen Netzwerktopologien untersucht. Formal ist ein solches Schedulingproblem gegeben durch ein Netzwerk, das durch einen Graph G=(V,E) mit Kantenkapazitäten c(e) repräsentiert wird, und eine Menge von Verbindungsanfragen, die jeweils durch ein Tupel (u,v,b,d) repräsentiert werden. Dabei sind u und v die Verbindungsendpunkte, b ist die benötigte Bandbreite, und d ist die Verbindungsdauer. Das Ziel ist, jeder Anfrage r einen Pfad P_r in G sowie einen Startzeitpunkt t_r zuzuordnen, wobei die Summe der Bandbreiten von gleichzeitig aktiven Verbindungen, die eine Kante e benutzen, deren Kapazität c(e) nicht übersteigen darf. Als Optimierungskriterium wurde die Gesamtlänge des Schedules gewählt. Das hat außerdem den Vorteil, daß automatisch auch der Durchsatz des Netzwerks optimiert wird. Weiterhin wird zwischen gerichteten und ungerichteten Verbindungen unterschieden. Gerichtete Verbindungen belegen die verwendeten Links nur in der Richtung vom Sender zum Empfänger, während ungerichtete Verbindungen alle verwendeten Links in beiden Richtungen belegen.
Das Schedulingproblem für Verbindungen ist interessant sowohl für Hochleistungs-Telekommunikationsnetze der Zukunft, in denen vielerlei Daten einschließlich Multimedia-Anwendungen und Video on Demand mit großem Datenvolumen und hohen Ressourcenanforderungen kommuniziert werden, als auch für parallele Anwendungen, die auf ATM-vernetzten Workstation-Clustern oder Parallelrechnern mit entsprechenden Verbindungsnetzwerken ablaufen. Ergebnisse für das Scheduling von Verbindungen, die einheitliche Dauern haben und die volle Bandbreite aller verwendeten Links belegen, lassen sich außerdem direkt auf das Problem der Wellenlängenzuteilung in optischen Netzen übertragen, wobei dann die Zeitschritte den Wellenlängen entsprechen.
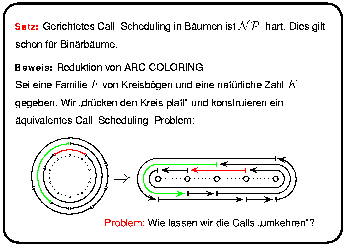
Im Berichtszeitraum konnte das Teilprojekt A7 bereits einige wichtige Resultate für das Scheduling von Verbindungen erzielen ([EJ96a], [EJ97]). Insbesondere konnte gezeigt werden, daß das Problem schon in sehr eingeschränkten Varianten NP-schwer ist, nämlich bei Verbindungen mit einheitlicher Dauer und einheitlicher Bandbreite in Bäumen (bei gerichteten Verbindungen schon in Binärbäumen, bei ungerichteten Verbindungen erst in Bäumen mit unbeschränktem Grad), Ringen und Gittern. Die meisten dieser Resultate wurden durch Reduktion des NP-vollständigen Problems ARC-COLORING (Garey, Johnson, Miller und Papadimitriou, 1980) auf die jeweilige Schedulingvariante gezeigt. Für den Fall des Scheduling von gerichteten Verbindungen in Bäumen konnte dadurch eine offene Frage, die von Mihail, Kaklamanis und Rao (1995) gestellt worden war, beantwortet werden:
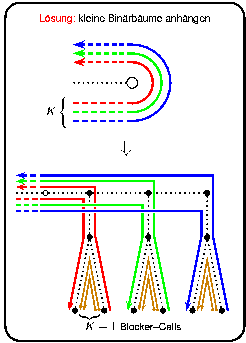
Optimale polynomielle Algorithmen existieren dagegen nur für Verbindungen mit einheitlicher Dauer und Bandbreite in Ketten (durch direkte Übersetzung von Algorithmen zur Färbung von Intervallgraphen (Slusarek, 1989), für ungerichtete Verbindungen mit einheitlicher Dauer und Bandbreite in Bäumen mit konstant beschränktem Knotengrad und für ungerichtete und gerichtete Verbindungen mit einheitlicher Dauer und Bandbreite in Bäumen, bei denen die Zahl der Verbindungen, die durch einen Knoten des Baumes laufen, durch eine Konstante beschränkt ist. Das erstgenannte Ergebnis für Bäume konnte durch die Entwicklung polynomieller Algorithmen zur Kantenfärbung von Multigraphen, deren Knotenzahl durch eine Konstante beschränkt ist (aber die trotzdem beliebig viele Kanten enthalten dürfen), erzielt werden [EJ97]. Hier führten die Ansätze dynamische Programmierung und ganzzahlige Programmierung mit konstant beschränkter Variablenzahl (Lenstra, 1981) zum Ziel. Der Algorithmus für den Spezialfall der konstant beschränkten Zahl von Verbindungen durch einen Baumknoten funktioniert durch Bearbeitung der Baumknoten in der Reihenfolge einer Tiefensuche, wobei für jeden Knoten alle möglichen Schedules der ihn betreffenden Verbindungen durchprobiert werden können [EJ97]).
Die besten bekannten Approximationsalgorithmen für Verbindungen mit
einheitlicher Dauer und Bandbreite liefern Güte 2
für Ringe (Raghavan und Upfal, 1994), Güte 1.1 für ungerichtete
Verbindungen in Bäumen (Nishizeki und Kashiwagi, 1990;
(
Ergebnisse für Verbindungen mit einheitlicher Dauer und Bandbreite sind
vor allem wegen ihrer Implikationen für die Wellenlängenzuteilung in
optischen Netzwerken von Bedeutung. Im Hinblick auf ATM-Netzwerke ist jedoch zu
erwarten, daß in der Praxis Verbindungen mit variablen Bandbreiten
und Dauern auftreten werden, die sich die von den ATM-Links zur Verfügung
gestellte Bandbreite teilen. Aus diesem Grund wurde in Teilprojekt A7
auch begonnen, diesen Fall genauer zu untersuchen. Variable Bandbreiten
machen das Problem bereits für einzelne Links NP-schwer,
variable Dauern bereits für Ketten (Reduktion von PARTITION, siehe
[EJ96a].
Daher beschränken sich die weiteren Untersuchungen hier
ausschließlich auf Approximationsalgorithmen und Online-Algorithmen.
Das Querschnittsprojekt Q4
Anwendungsintegrierte Lastverteilung (ALV)
im SFB 342 ist ein wichtiges Forum, in dem verschiedene Teilprojekte
des SFB 342 gemeinsame Fragestellungen bezüglich der Lastverteilung
in parallelen Programmen untersuchen. Die Kooperation der Teilprojekte
kann folgendermaßen eingeteilt werden:
In der Anlaufphase dieses Querschnittsprojektes haben die Teilprojekte
ihre laufenden Arbeiten in einer Vortragsreihe präsentiert.
In intensiven Diskussionen wurde klar, daß bei einer Ausrichtung auf
rein anwendungsintegrierte Lastverteilung wichtige Faktoren,
insbesondere in heterogenen Systemen mit Fremdlasten, zu wenig
Berücksichtigung finden. Zudem ist die vollständige Integration
der Lastverteilung in das Anwendungsprogramm wegen des zu großen
Implementierungsaufwandes oftmals unerwünscht. Besonderer Wert
muß daher auf eine gut organisierte Kooperation aller an der
Lastverteilung beteiligten Komponenten (Betriebssystem, Laufzeitsystem,
Anwendung) gelegt werden.
Es ist daher sinnvoll, im Rahmen des Querschnittsprojektes Q4 von
anwendungsbezogener Lastverteilung zu sprechen.
Darüber hinaus wurde schnell klar, daß das Lastverteilungsproblem
sowohl aus System- wie auch aus Anwendersicht sehr vielfältig ist.
Auch für Spezialisten auf diesem Gebiet ist es aufgrund einer
Vielzahl von Veröffentlichungen und Arbeiten zu diesem Thema schwierig,
sich einen Gesamtüberblick zu verschaffen.
Vor allem ist die Vergleichbarkeit der verschiedenen Strategien in
Bezug auf Performance und Einsetzbarkeit kaum gegeben.
Hieraus ergibt sich die Notwendigkeit eines umfassenden
Klassifikationsschemas für Lastverteilungssysteme,
das bereits bestehende Klassifikationen, z.B. von
Wang und Morris (1985), von Casavant und Kuhl (1988), von
Shivaratri, Krueger und Singhal (1992) und von Ludwig (1993),
um wichtige Aspekte erweitert und neueren Entwicklungen Rechnung trägt.
Für Anwender und Systementwickler soll dieses Klassifikationsschema
eine Entscheidungshilfe und Richtschnur für die Bewertung und
Entwicklung von Lastverteilungssystemen sein.
Es bildet den ersten Teil des Buches
Dynamic Load Distribution for Parallel Applications
(Schnekenburger und Stellner (Hrsg.), Bd. 24 der Reihe
TEUBNER TEXTE zur Informatik, Tuebner Verlag, 1997)
das vom Querschnittsprojekt Q4 verfaßt wurde.
Das Klassifikationsschema umfaßt im einzelnen:
Der Beitrag des Teilprojektes A7
[BE97]
zu obengenanntem Buch ist die
Klassifikation der Lastverteilungsstrategien, sowie eine Übersicht
ausgewählter Algorithmen und deren Einordnung in das Schema.
Die Klassifikation gliedert sich in 5 Hauptgruppen, deren Kriterien
hier kurz zusammengefaßt sind:
Da eine vollständige Übersicht bekannter Lastverteilungsstrategien
aufgrund ihrer Vielzahl kaum sinnvoll erschien und zudem den
zur Verfügung stehenden Rahmen gesprengt hätte, wurden
Diffusion (Cybenko, 1989) und Bidding (Stankovic und Sidhu,
1984; Radermacher, 1996) als bekannte und erprobte Strategien sowie die
Lastverteilung durch Random-Matchings (Ghosh und Muthukrishnan, 1994)
und Precomputation-Based Loadbalancing
(Böhm und Speckenmeyer, 1996) als neuere Ansätze
exemplarisch dargestellt. Dabei wurde vor allem versucht,
die algorithmischen Ideen dieser Strategien deutlich zu machen.
In der Vergangenheit wurde primär das sog. Packet-Routing
eingesetzt, bei dem die auszutauschenden Nachrichten komplett in einem
Stück
verschickt werden. Das kann natürlich negative Auswirkungen haben, wenn es
sich um lange Nachrichten handelt: jeder Prozessor, der von dem Weiterleiten
der Nachrichten betroffen ist (also diejenigen, die auf dem Weg liegen, den
die Nachrichten vom Sender zum Ziel zurückzulegen haben), muß
entsprechenden Pufferspeicher zur Verfügung stellen.
Einen anderen Weg geht das Wormhole-Routing: Die Nachrichten werden in
kleine Stücke aufgeteilt, die dann hintereinander vom Sender zum Ziel
transportiert werden (``wurmartig''). Dabei ist es je nach Modell einem
solchen Wurm erlaubt oder verboten, sich zu trennen oder etwa sich
zusammenzuziehen. Natürlich hat auch dieses Verfahren Nachteile, so lassen
sich etwa Situationen vorstellen, in denen sich mehrere solcher Würmer
derartig gegenseitig blockieren, so daß für keinen mehr ein
Weiterkommen möglich ist. Es ist Aufgabe des Routing-Algorithmus, solche
Fälle auszuschließen.
Es gibt mittlerweile einige Arbeiten über Wormhole-Routing. Von
Felperin, Raghavan und Upfal (1992) wurde Wormhole-Routing auf
(n × n)-Gittern betrachtet,
wobei davon ausgegangen wird, daß initial jeder Prozessor eine Nachricht
verschickt, für die ein zufälliges Ziel
gewählt wird. Wenn die Nachrichten aus je L einzelnen Teilpaketen
bestehen, kann die Laufzeit zu O(n*L*log(n))
abgeschätzt werden. Diese Schranke gilt mit hoher Wahrscheinlichkeit
(m.h.W.), d.h. die Wahrscheinlichkeit, daß der Algorithmus länger
braucht, ist polynomiell klein.
In einer an der Universität Paderborn angefertigten Diplomarbeit wurde
gezeigt, daß dieses Verfahren für mehrdimensionale Gitter erweitert
werden kann. Unter gleichen Voraussetzungen (von jedem Prozessor startet eine
Nachricht mit zufällig gewähltem Ziel) wird für das
d-dimensionale Gitter mit Kantenlänge n (auch:
(n,d)-Gitter) eine Laufzeit von
O((L+d)*n*log(n)) (m.h.W.) bewiesen, falls
d <= n/log(n) und
L <= n/((d-1)*log(n) gilt.
Ein anderer Weg wird von Scheideler und Vöcking (1996) gegangen. Es wird
ein dynamischer universeller Wormhole-Algorithmus vorgestellt, der auf
beliebigen Topologien arbeitet. Dynamisch heißt hier, daß die
Nachrichten nicht am Anfang in den Knoten des Netzwerks vorliegen, sondern mit
einer bestimmten Injektionsrate erzeugt werden. Falls diese
B/(12*e*L*n*(2d)(1/B))
nicht übersteigt, wird jeder Wurm im (n,d)-Gitter
in erwarteter Zeit
O(n*d+L)
zugestellt. Dabei steht B für die Bandweite
eines Links, d.h. die Anzahl Pakete, die gleichzeitig über einen Link
ziehen dürfen.
In allen Ansätzen ist von zufälliger Verteilung der Ziele ausgegangen
worden. Das ist aber in der Praxis nicht immer der Fall. Insbesondere
bei wissenschaftlichen Anwendungen kann häufig ein systematischer
Kommunikationsverlauf beobachtet werden. Ziel weitergehender Forschung
könnte sein, Routing-Protokolle zu entwickeln, die das Vorhandensein eben
dieser Struktur ausnutzen, um damit mehr Effizienz zu erlangen.
Außerdem sehr interessant ist sicherlich, die Annahme einer
zufälligen Auswahl eines Ziels zugunsten der Existenz eines
``Gegenspielers''
fallenzulassen, unter Beibehaltung des dynamischen Charakters. Aktuelle
Arbeiten im Bereich Packet-Routing unterstützen diese These. Man kann sich
darunter eine Situation vorstellen, in der ein Gegenspieler Nachrichten ins
Netz injiziert, wobei ihm allerdings bezüglich der Anzahl der
einzuspeisenden
Nachrichten pro Zeitintervall und der entstehenden Pfadüberschneidungen
Einschränkungen gemacht werden. Die sich jetzt stellende Frage ist
natürlich wieder, wie stark der Gegenspieler eingeschränkt werden
muß, um zusichern zu können, daß alle eingespeisten
Nachrichten in bestimmter Zeit zum Ziel transportiert werden.
Eine weitere sehr interessante (und aktuell stark untersuchte) Richtung ist
das sog. Circuit-Routing. Im zugrundeliegenden Modell wird davon
ausgegangen, daß die Kosten der Kommunikation zweier Prozessoren nicht
mehr proportional mit der Entfernung steigen. Inspiriert wird dieses Vorgehen
durch aktuelle Entwicklungen im Bereich der Highspeed-Kommunikation (vgl.
ATM), wo in der Tat keine signifikanten Mehrkosten durch größere
Entfernungen mehr auftreten. In diesem Bereich ist die Frage, ob praktikable
und effiziente Algorithmen für (insbesondere mehrdimensionale) Gitter
existieren, nicht geklärt.
Als Folge der zunehmenden Verbreitung von ATM-Netzen ergibt sich
außerdem ein neues Einbettungsproblem. In einem ATM-Netzwerk
ist es nämlich möglich, über der gegebenen physikalischen
Netzwerktopologie eine sogenannte virtuelle Topologie
einzurichten. Dies erfolgt mit Hilfe von virtuellen
Pfaden (Cidon, Gerstel und Zaks, 1994; Gerstel, Wool und Zaks, 1995). Wenn
die virtuelle Topologie gewisse Nebenbedingungen erfüllt
(z.B. beschränkte Zahl der virtuellen Pfade pro physikalischer
Verbindung), verhält sich das System vergleichbar einem
System, das die Topologie hardwaremäßig implementiert.
3.5 Klassifikation von Lastverteilungsstrategien
Die enorme Rechenleistung und die zunehmende Verfügbarkeit
paralleler und verteilter Systeme eröffnet die Möglichkeit,
immer komplexere Probleme in vertretbarer Zeit zu lösen.
Bei vielen Anwendungen entwickelt sich die Lastverteilung in
solchen Systemen in unvorhersehbarer Weise.
Dies kann dazu führen, daß die Gesamtlaufzeit eines
parallelen Programms durch wenige überlastete Rechenknoten bestimmt wird.
Effiziente dynamische Lastverteilungsalgorithmen
zum Ausgleich von Lastungleichgewichten sind daher unentbehrlich.
Allgemeine Klassifikation
Zielrichtung, Integrationsebene und Struktur von Lastverteilungssystemen.
Klassifikation von Lastverteilungsstrategien
Beschreibung siehe unten.
Klassifikation von Lastmodellen
Im Gegensatz zu bisherigen Arbeiten
soll an Stelle der exemplarischen Beschreibung von Last-Indizes eine
Klassifikation der Lasterfassungskomponenten und der Beziehungen zur
Lastverteilungsstrategie treten.
Klassifikation von Migrations-Mechanismen
Dieser wichtige Teilbereich findet bei der Spezifikation von
Lastverteilungsstrategien oft nur wenig oder gar keine
Berücksichtigung, ist jedoch für die Performance des
Lastverteilungssystems von größter Bedeutung.
System-Modell
Topologie der Maschine und der Anwendungsobjekte, sowie Motivation der
Strategie.
Transfer-Modell
Distanz von Lastverschiebungen zwischen zwei Rechenknoten und
Unterscheidung von unterbrechender/nicht-unterbrechender Verschiebung.
Informations-Austausch
Distanz des Informationsaustausches zwischen zwei Rechenknoten und
Bewertung des Informationsstandes einer Entscheidungsinstanz.
Koordination
Struktur und Art der Entscheidungsfindung und
Reichweite einer Lastverteilungsaktion.
Algorithmus
Art des Entscheidungsprozesses, Initiierung der Lastverteilung,
Adaptivität, Kostensensibilität und Stabilitätskontrolle.
3.6 Routing in schnellen Netzen
Betrachtet man den Ablauf paralleler Algorithmen auf Mehrprozessorsystemen,
so stellt man fest, daß i.a. ein großer Teil der kompletten
Laufzeit für Kommunikation der Prozessoren (Routing) untereinander
aufgewendet werden muß. Deshalb ist es sinnvoll und notwendig, effiziente
Kommunikationsstrategien zu entwickeln.