"Erste Ansätze für Suchalgorithmen"

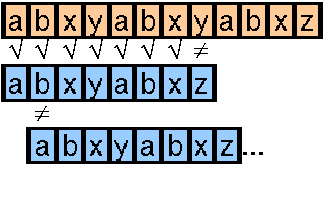
Wenn man sich mit dem Problem des Suchens von Zeichenketten in Texten befaßt, kann man den Aufwand (die Anzahl der Vergleiche) durch geschicktes Anwenden vergleichreduzierender Methoden drastisch senken.
Sei ´n´ die Länge des Suchmusters und ´m´ die Länge des zu durchsuchenden Textes. Bei Benutzung der verbesserten Verfahren ist es möglich die Größenordnung der Anzahl an Vergleichen von O(n x m) auf O(n + m) zu verringern!

1. Die "naive" Methode:

Vergleicht man Suchmuster und Text Zeichen für Zeichen von links nach rechts und schiebt man das Suchmuster bei einem Mismatch um ein Zeichen weiter nach rechts, so benötigen wir schlimmstenfalls (falls in Suchmuster und Text nur gleiche Zeichen vorkommen; z.B. lauter ´a´s) n mal (m - n + 1) Vergleiche.
In diesem Fall hat die Anzahl der Vergleiche also die Größenordnung O(n x m).

2. Eine bessere Methode:

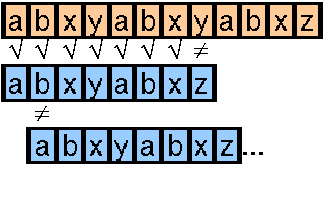
Man verfährt wie bei der naiven Methode. Nur wird bei einem Mismatch nicht immer um ein Zeichen weitergeschoben, sondern bis zu der Stelle, wo das erste Zeichen des Suchmusters (im Beispiel ´a´) innerhalb der schon verglichenen Zeichen im Text noch einmal vorkommt. Kommt es dort nicht vor, so schieben wir den Anfang des Suchmusters bis zur Stelle des Mismatches.
Im Beispiel sparen wir uns dadurch schon ganze drei Vergleiche gegenüber der naiven Methode.

3. Eine noch bessere Methode:

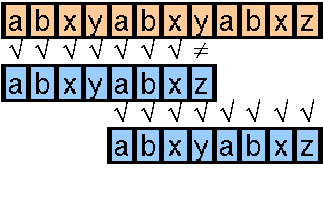
Noch weniger Vergleiche benötigt man, wenn man bei einem Mismatch zum nächsten bekannten Vorkommen der ersten drei Zeichen vorrückt und diese dann nicht nochmal vergleicht (wir wissen ja bereits, daß an diesen Stellen eine Übereinstimmung besteht), sondern erst beim vierten Zeichen des Suchmusters weitervergleicht.
Dadurch benötigen wir noch einmal drei Vergleiche weniger als bei der vorigen Methode.

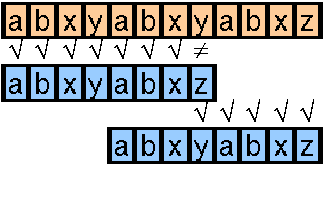
Man sieht also, daß man durch Wissen über den Aufbau des Suchmusters Vergleiche sparen und damit die Geschwindigkeit des Algorithmus drastisch erhöhen kann.
Dies erreicht man in der Praxis durch Preprocessing des Suchmusters (Manche Algorithmen wenden das Preprocessing auch auf den Text an). Ein besonders fundamentaler Preprocssing-Algorithmus - den auch wir verwenden werden - arbeitet mit sogenannten "Z-boxes", die auf der nächsten Folie behandelt werden.