"Z-Boxes"

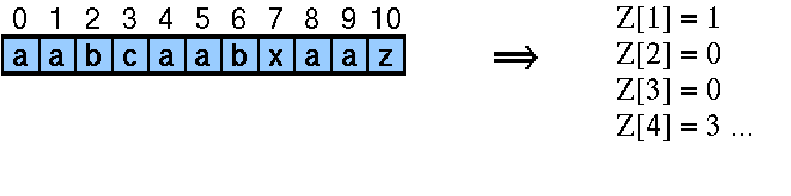
Definition: Eine Z-box Z[pos] beinhaltet die längste Zeichenkette die eine Kopie eines Präfix des Suchmusters ist und an der Position pos beginnt.
Im Beispiel beginnt an der Position ´4´ eine Z-box der Länge drei, weil "aab" auch im Präfix des Suchmusters vorkommt.

Ein Beispiel:

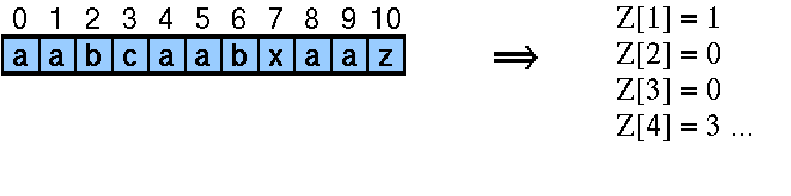
Allein mit Hilfe des Z-Algorithmus, der die Z-boxes in linearer Zeit berechnet, kann man den einfachsten bekannten Suchalgorithmus konstruieren, der in linearer Zeit abläuft.
Hierzu nimmt man das Suchmuster und fügt es vorne an den zu durchsuchenden Text an. Dann sucht der Z-Algorithmus von links nach rechts nach Z-boxes, die genau die länge des Suchmusters haben. Dies sind dann die Vorkommen des Suchmusters im Text.
Um zu gewährleisten, daß der Algorithmus nur Vorkommen im eigentlichen Text und nicht schon davor findet, müssen Suchmuster und Text durch ein Zeichen getrennt werden, das in keinem von beiden vorkommt.
Wie man später sehen wird, können alle Z-boxes in einer Zeit von O(n + m) = O(m) berechnet werden.

Im Folgenden werden wir diesen Z-Algorithmus betrachten. Da der Boyer-Moore Algorithmus allerdings mit spiegelverkehrten Z-boxes arbeitet, wollen wir auch den spiegelverkehrten Z-Algorithmus betrachten. Zur Unterscheidung reden wir dann von "N-boxes" und "N-Algorithmus". Der Z-Algorithmus funktioniert aber völlig analog.